Photon and dark signal transfer curves
A photon transfer curve can be used to show many important features of a camera's response to illumination, in particular the gain and the full-well limit. A photon transfer curve is obtained by taking a series of pairs of uniformly illuminated exposures. Each pair of light frames is made for the same exposure time, but the exposure time is varied from pair to pair. The signal level and noise are determined for each pair of exposures and the noise is plotted against the signal on logarithmic axes. The technique is described in detail in "Photon Transfer DN -> Lambda" by James R. Janesick, ISBN 978-0-8194-6722-5 and is discussed briefly below.
In summary, the total noise (in ADU) for an exposure is given by:
![]()
where the total noise is obtained by taking the square root of the quadrature sum of the individual noise components:
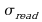 is the read noise
is the read noise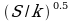 is the shot noise in ADU arising from the photon flux; S is the signal (number of counts in ADU) and k is the gain in electrons/ADU. (Suppose the total number of photons per pixel in an exposure is N and assume that each photon results in one electron. Then the number of electrons is N, and the shot noise is the square root of N i.e. sqrt(N). When the number of electrons is converted to ADU, the signal in ADU becomes S = N/k but the noise is now sqrt(N)/k, because the 'width' of the gaussian shot noise distribution is scaled by the same factor as the mean value. Since N = S x k, the noise in ADU is sqrt(S/k)).
is the shot noise in ADU arising from the photon flux; S is the signal (number of counts in ADU) and k is the gain in electrons/ADU. (Suppose the total number of photons per pixel in an exposure is N and assume that each photon results in one electron. Then the number of electrons is N, and the shot noise is the square root of N i.e. sqrt(N). When the number of electrons is converted to ADU, the signal in ADU becomes S = N/k but the noise is now sqrt(N)/k, because the 'width' of the gaussian shot noise distribution is scaled by the same factor as the mean value. Since N = S x k, the noise in ADU is sqrt(S/k)).- FPN x S is the fixed pattern noise arising from non-uniformity of response of the CCD chip. (Suppose we consider two neighbouring pixels where one has half the sensitivity of the other. If one exposure resulted in 100 counts in one pixel and 200 in the other, an exposure of twice the length would give 200 and 400 counts respectively. So the fixed pattern noise scales linearly with the signal).
The three parts of the total noise equation can be separated out by analysis of the pairs of light frames (in practice, a subset of each frame, say 100 to 200 pixels on side, is used rather than the whole chip area). The average number of counts for each pair (with the bias offset removed) gives the mean signal, the average standard deviation for each pair gives the total noise and the standard deviation of the difference of each pair, divided by sqrt(2), gives the read noise plus shot noise (the fixed pattern noise is removed by the differencing process). The fixed pattern noise can then be calculated from the total noise equation. If the read noise is known (e.g. from bias frame analysis), the shot noise can be separated out from the read-plus-shot noise. (The read noise can also be estimated from the photon transfer curve). Each pair of exposures thus gives one value for the mean signal, total noise, shot noise and fixed pattern noise.
Photon transfer curve
A white-light LED light box was used for the illumination and the CCD was maintained at -15C for the transfer curve measurements. The signal and noise values were derived from a central area of the chip where the illumination was uniform and are plotted on the graph below. Note how the total noise plot (blue line) falls into three distinct parts. To the left, there is a horizontal part with slope of zero where the read noise dominates, then a slope of one half (parallel to the orange line) where the shot noise dominates, and just visible at the top of the total noise curve, a slope tending towards one (parallel to the green line) where the fixed pattern noise dominates.

The gain and fixed pattern noise are deduced by fitting the equations for shot noise and fixed pattern noise to the data. (If the x-axis is drawn to intercept the y-axis at 1, then the gain and fixed pattern noise can also be found by graphical means by reading the intercept of the corresponding line on the x-axis). An average value of 1.33 e/ADU is found for the gain if fitting over the range 1000 - 40000 ADU, but increases slightly at higher signal levels. This is to be expected from the linearity measurements. There appears to be some deviation from the straight-line fit to the shot noise at low numbers of counts; this may be due to uncertainty in the calculation of the shot noise from the measured read-plus-shot noise, or arise from variations in the gain.
The sharp turn-over point for the transfer curves implies that full well is first reached at 53000 ADU. Streaking becomes increasingly visible on the light frames above this level, indicating that some of the CCD wells are starting to saturate. For a gain of 1.33 e/ADU, this implies a full well level of about 70,000 electrons.
The fixed pattern noise within the chosen 128 pixel square has a very low value of about 0.19% and appears to originate from the vertical banding evident in high contrast flat field frames. The Kodak specification gives a nominal value of 1% for the photoresponse non-uniformity when comparing squares of 128 pixels on a side. Even this seems pessimistic; flat field data suggest that the typical deviation is about 0.25% at most.
It is usual to ignore the influence of the dark signal for photon transfer analysis because dark subtraction adds undesirable noise. To check the validity of this approach, the analysis was repeated by applying the 'normal' pixel mask to the data (see the dark signal analysis for details). This selects only those pixels with a dark signal so low that it can truly be ignored, even for the longest exposures of 30 seconds used here. The difference was negligible; even for the longest exposures, the original data-set without any allowance for dark signal had a mean signal of about 0.5 ADU more than the dark-adjusted set, with a total noise component about 0.2 ADU higher).
Dark signal transfer curve
A similar procedure can be followed for dark frames. A sequence of pairs of dark 'exposures' was made at +15C (to give sufficient dark signal) with a maximum exposure time of four hours. An area of the chip with apparently few hot pixels was chosen for the analysis. This gave a fixed pattern noise of about 50% which suggested that the hot pixels were still dominating the result. The 'normal pixel' mask (see the dark signal analysis for details) was then applied to give the transfer plot shown below.
The dark response non-uniformity is about 3% for the majority of pixels. The shot noise line isn't a fit to the data; it's the expected line for the gain of 1.33 found for the light frame data.
