Linearity
CCDs are generally linear devices, which makes them ideal for photometric applications. The KAF-3200ME chip used in this camera is non anti-blooming and should show good linearity characteristics over most of its range. This investigation attempts to measure the non-linearity and demonstrates the effeciveness of applying a linearity correction to a pair of images.
Linearity response
There are various ways of measuring non-linearity. Most methods involve exposing the CCD to a given number of photons at each step and varying the number of photons in a known way from step to step. The number of photons per step can be governed by the duration of the CCD exposure, the time for which the light source is on, or the length of time between clocking successive rows of the CCD. The measured number of counts per step is plotted against the duration of illumination for each step to obtain the linearity response. Sometimes a ratio method is used, where one non-uniformly illuminated exposure is divided by another and the parameters of the assumed linearity response are adjusted until a completely flat image is obtained.
Probably the simplest method is to use a constant light source and make exposures of varying duration. This was adopted here, using a white-light LED light box. The accuracy is limited by the variability of the light source and errors in the shutter timing. In practice it proved harder than expected to obtain a satisfactory result; see the following section for a more detailed discussion. A linearity curve constructed from a good set of measurements at -25C is shown below.
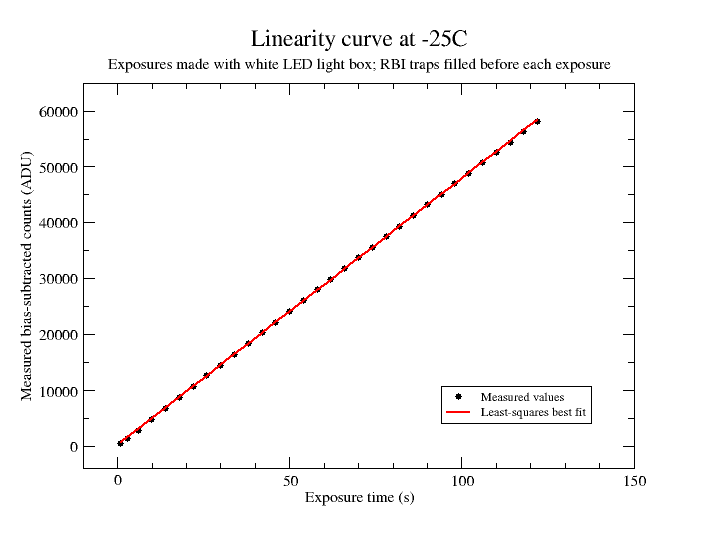
The linearity response is very good, but close inspection reveals a smooth shallow curve. A straight line fit through the measured points is shown in red. The points lie below the line at low and high counts, and above the line in the middle of the range. Note that this can be misleading: the measured points must scatter each side of the line by the nature of a least squares best fit; whereas the true non-linearity curve is shown below to be a steady decline from the expected linear response, rather than deviating each side of it.
Accurate measurement of non-linearity parameters
The linearity response is difficult to measure accurately because RBI effects and likely variations in light source intensity can be of a similar magnitude to the camera non-linearity. (This is one situation where we are trying to make an absolute photometric measurement, so RBI effects are important). Early attempts at measuring the linearity response failed because the short exposures of 500 to 1000 ADU were significantly reduced (i.e. of the order 1% to 2%) by trapping of some photo-electrons in the substrate rather than in the CCD wells.
Eventually it was decided to pre-fill the RBI traps to their highest level by 'pre-flashing' the camera with unfiltered light from the light box before each linearity measurement. To make this more successful, the camera temperature was lowered to -25C since the decay time of the traps increases with decreasing temperature and thus they stay full for longer. [Note: If trap decay cannot be completely prevented, the best approach is to pre-fill the traps to their equilibrium level for the chosen light intensity, rather than filling them completely; this way the error can be made arbitrarily small. However, it would have taken a minute or so for the traps to reach equilibrium at the intensity used for the linearity measurements and thus made the entire sequence very long. There is a trade-off between reducing the error from RBI effects and keeping the sequence short to minimise the effect of long-term variations in the light source].
The LED light box and power supply were turned on some time before the start of the measurements to allow time for them to stabilise thermally. The sequence of measurements was repeated continuously overnight and sequences were selected where the light source had apparently remained stable to within 0.1% over the course of a sequence. The median of a central, uniformly illuminated part of each light frame measuring 150 by 50 pixels was taken after bias-subtraction. The value thus obtained was divided by the length of the exposure to obtain an effective flux in counts per second. Variations in the flux are taken to be an indication of non-linearity. Each selected sequence was normalised by dividing by the mean flux for the entire sequence (but excluding the first four measurements at 1s, 3s, 6, and 10s) and the results are plotted in the graph below.
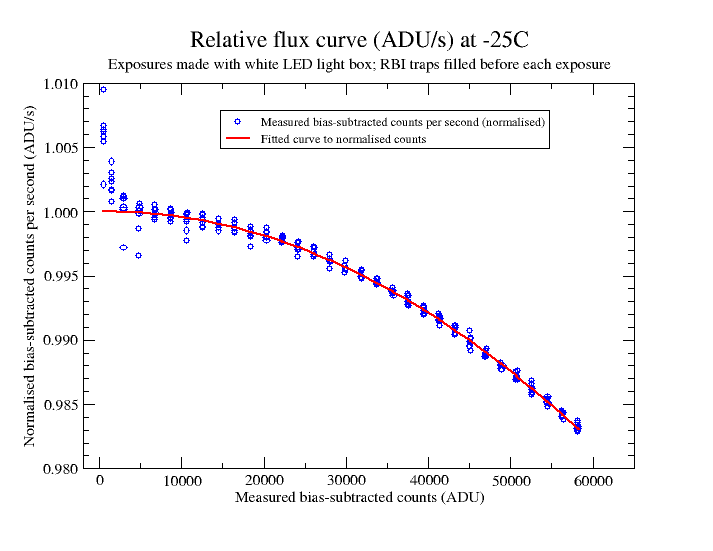
The first three groups of measurements corresponding to the exposures of 1s, 3s and 6s clearly lie above the fitted line, whilst the fourth group of measurements at 10s lies just above the line. Clearly these measurements are influenced by RBI trap decay from their preceding pre-flash exposures. To test the likely effect of trap decay on these groups of points, a series of 'pre-flash' exposures was made and each exposure was followed by a dark frame of a length corresponding to one of the exposures that was used for the linearity measurements. The counts due to decay of the traps were found to be 3.0 ADU for a 1s dark frame, 4.4 ADU for a 3s dark frame, 6.0 ADU for a 6s dark frame and 7.3 ADU for a 10s dark frame. For exposures longer than 10s, the proportion of trap-decay electrons relative to the number arising from the light frame exposures was found to be negligible, so the red curve was fitted after omitting the exposures from 1s to 10s. Finally, the curves were re-nomalised to give a relative flux of 1.0 for zero counts (after bias subtraction).
If the true counts are given by T and the measured counts by M, then:
where f(M) is the equation for the fitted curve shown by the red line above:
In comparison, Christian Buil finds coefficients of 1.0007, -1.8712E-08 and -5.0816E-12. The coefficients calculated here imply a flux of 0.9820 at 60000 ADU relative to zero ADU, whereas Christian Buil's values give 0.9806. The agreement is very good and implies a high degree of consistency between cameras.
Note that the decrease in the apparent photon flux at high signal levels is a sign of an increase in gain (i.e. an increase in electrons per ADU); more electrons (and hence more photons) are required to give a count of 1 ADU at high signal levels. Since the actual number of photons (electrons) per second remains the same, the measured number (in ADU) must decrease.
Correction for non-linearity
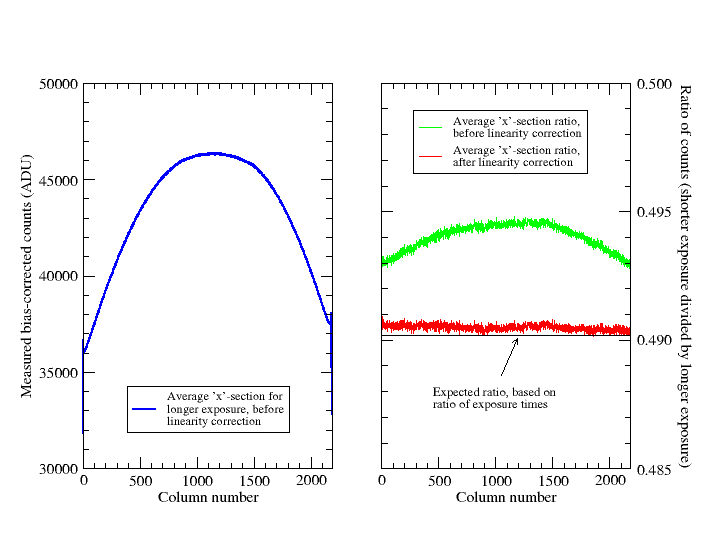
To examine the effect of correcting for non-linearity, the ratio of two light frames was taken, before and after correction. The light frames had a significant variation in brightness across the frame in both directions. The left-hand graph below shows the average 'x'-section through the frame with the higher counts, before correction.
The right-hand graph shows in green the average 'x'-section of the ratio frame obtained by dividing the shorter exposure by the longer one, before correction for non-linearity. The red line shows the average 'x'-section after correction of the two individual frames for non-linearity. The red line is much flatter. The horizontal line just below the red line shows the expected value based on the ratio of shutter times for the two exposures, on the assumption of a completely constant light source and no shutter timing errors. The mean value of the red line is higher than the expected value by 0.06%. This value is indicative of the sort of photometric accuracy that can be expected with this camera, at least under laboratory conditions.