King's polar drift method
In the second part we saw the influence of refraction on the precision of the elevation adjustment of a mount, and how it affects the elevation at which the mount actually ends up pointing. In fact it seems rather tricky to make a reliable adjustment by the standard drift-alignment method at all. But there is another method that accurately aligns the telescope mount with the refracted pole, provided that there is a clear view of the immediate area.
In his book "A Manual of Celestial Photography", E.S.King describes a method of polar alignment dependent on photographing polar star trails arising as a result of a misaligned mount. Consequently this method results in aligning the telescope mount with the visual location (and hence refracted position) of the pole. Once again, the purpose is to adjust the the mount until no trails are seen.
For small displacements of the telescope's polar axis and in a region close to the pole, King found stars to drift in arcs of circles whose radius is equal to the offset of the telescope mount's polar axis from the observed position of the true pole. Better yet, the direction of offset is perpendicular to the arc of the circle, on its concave side. So in principle this method gives a quick and accurate means of determining the amount and direction of offset. This can be understood as follows.
Polar misalignment and polar star trails
Imagine standing looking up at the pole with stars circling around it. Suppose that a telescope mount is offset a distance o from the true pole P, such that the projection of the telescope mount's polar axis on the sky is at position T, as shown in the diagram below. The diagram shows the mount offset beneath the pole, but by rotating the diagram about the true pole, clearly it could be in any direction. A star lies a distance r from the true pole and rotates about it anti-clockwise. (This applies for the north pole; for the south pole, the direction of motion is reversed). The green rectangle represents an imaging area for a camera attached to the telescope mount that is attempting to track the star. This rotates about the telescope mount pole anti-clockwise, also at the sidereal rate.
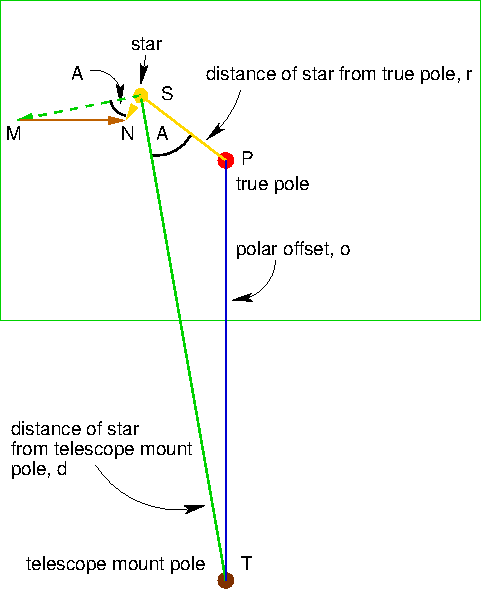
Usually when we view the sky we are looking at stellar motion all around us, as though looking out
from the inside of a dome. But in the area close to the pole we see stellar motion 'face on', i.e. as if
projected onto a flat plane. In this plane view, if the sidereal rate is ![]() radians per second, then in a small time interval
radians per second, then in a small time interval ![]() the star moves a distance
the star moves a distance ![]() from S to N, where the angle PSN is a right-angle. (The distance moved is greatly exaggerated for clarity). Now imagine a point on the image sensor at the same initial location as the star and at some distance d from the telescope mount pole at the start of the image exposure. This point rotates about the telescope mount pole at this fixed distance d at the sidereal rate and moves a distance
from S to N, where the angle PSN is a right-angle. (The distance moved is greatly exaggerated for clarity). Now imagine a point on the image sensor at the same initial location as the star and at some distance d from the telescope mount pole at the start of the image exposure. This point rotates about the telescope mount pole at this fixed distance d at the sidereal rate and moves a distance ![]() from S to M in the same time that the star moves from S to N, where the angle TSM is a right-angle. Since PSN is a right-angle and PST equals some initial angle A, TSN equals 90 degrees minus A. But since TSM is also a right-angle, NSM must equal 90 - (90 - A) degrees, i.e. NSM equals A. Therefore triangles TPS and MNS are similar, so the distance MN equals
from S to M in the same time that the star moves from S to N, where the angle TSM is a right-angle. Since PSN is a right-angle and PST equals some initial angle A, TSN equals 90 degrees minus A. But since TSM is also a right-angle, NSM must equal 90 - (90 - A) degrees, i.e. NSM equals A. Therefore triangles TPS and MNS are similar, so the distance MN equals ![]() . In other words, relative to point M, the star has appeared to move a distance
. In other words, relative to point M, the star has appeared to move a distance ![]() in a direction perpendicular to the direction of the offset of the telescope mount from the pole and clockwise in the plane of the sky. Note that since this is independent of the star's distance from the pole, the same drift is observed for all stars in the field, even at the pole itself.
in a direction perpendicular to the direction of the offset of the telescope mount from the pole and clockwise in the plane of the sky. Note that since this is independent of the star's distance from the pole, the same drift is observed for all stars in the field, even at the pole itself.
To understand the long-term apparent stellar motion, we need to consider the rotation of the image sensor. The point M represents the point on the sensor at which the image of the star was initially registered at the start of the exposure. During the period ![]() , the image sensor has also rotated anti-clockwise about the telescope mount pole by an angle
, the image sensor has also rotated anti-clockwise about the telescope mount pole by an angle ![]() . So the apparent position of the star relative to its initial
point on the image sensor has moved right by an amount
. So the apparent position of the star relative to its initial
point on the image sensor has moved right by an amount ![]() and downwards at an angle
and downwards at an angle ![]() .
This process is repeated from the star's new position on the image sensor for the next instant
.
This process is repeated from the star's new position on the image sensor for the next instant ![]() and so the star gradually appears to make a circle of radius o, with the circle's diameter extending from the star's initial position in the direction of the offset of the telescope mount from the true pole. This sequence of events is shown in the diagram below.
and so the star gradually appears to make a circle of radius o, with the circle's diameter extending from the star's initial position in the direction of the offset of the telescope mount from the true pole. This sequence of events is shown in the diagram below.

The star is initially at position 0 with the image sensor horizontal (position P). Imagine the lines X, Y and Z to be drawn on the image sensor at an angle ![]() to each other when the sensor is at position P, with line X initially horizontal. During the first interval
to each other when the sensor is at position P, with line X initially horizontal. During the first interval ![]() , the star appears to move right by a distance indicated by the first brown arrow, but at the same time the sensor rotates anti-clockwise by angle
, the star appears to move right by a distance indicated by the first brown arrow, but at the same time the sensor rotates anti-clockwise by angle ![]() to bring the star to apparent position 1 on the sensor, which is now at position Q. Furthermore, the line Y will have rotated anti-clockwise so that it is now horizontal. The process thus repeats in the next interval
to bring the star to apparent position 1 on the sensor, which is now at position Q. Furthermore, the line Y will have rotated anti-clockwise so that it is now horizontal. The process thus repeats in the next interval ![]() to move the star to apparent position 2 on the sensor, now at position R. This eventually produces a full circle.
to move the star to apparent position 2 on the sensor, now at position R. This eventually produces a full circle.
For short duration exposures we obtain small arcs of circles, with the radius pointing from the arc in the direction of the polar offset. In the northern hemisphere these arcs proceed clockwise and in the southern hemisphere they proceed anti-clockwise, but in brief exposures of a few minutes typical for this polar alignment technique, the arcs are likely to be short enough to appear like straight lines.
Since the length, l, of the arc is ![]() , we can easily calculate the offset of the mount from the pole by:
, we can easily calculate the offset of the mount from the pole by:
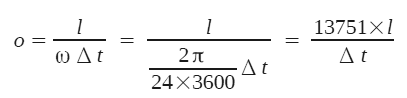
where ![]() is in seconds and for small angles, the length of the arc can be expressed in arc seconds or arc minutes to give the corresponding offset in the same units. Note that this expression is exactly the same as the one that we derived for the polar offset in terms of the maximum drift rate (MDR) for the standard drift alignment technique. So the polar drift method has the same precision as normal drift alignment.
is in seconds and for small angles, the length of the arc can be expressed in arc seconds or arc minutes to give the corresponding offset in the same units. Note that this expression is exactly the same as the one that we derived for the polar offset in terms of the maximum drift rate (MDR) for the standard drift alignment technique. So the polar drift method has the same precision as normal drift alignment.
Polar drift in practice
Since the size of the polar offset is easily calculated from the length of the star trail and the direction of the offset can be deduced from the orientation of the trail, the correct adjustment can in principle be made immediately. But it must be remembered that a movement of, say, 1 degree in azimuth for the telescope mount generally has less effect than a movement of 1 degree in elevation (see the discussion of normal drift alignment), so making a single adjustment of the correct size in the right direction is difficult to do. Some iterative technique is likely to be necessary in practice. A fascinating alternative perspective on stellar drift, with examples of polar trails and the demonstration of such an iterative technique is given in Nathan Towne's study of this method.
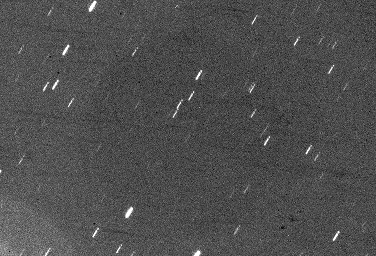
Some care is needed if using the orientation of the drift trail to deduce and adjust the direction of the polar offset, as can be seen in the following two images. These were taken with a Starlight Xpress Lodestar at an image scale of about one arcsec per pixel. Each image was interrupted for a brief period near the beginning so that the sense of the drift could be determined (King suggests turning off the telescope tracking at the end of each exposure instead - this may work better for very short trails where a brief interruption could be hard to see).
The first image shows trails obtained with the polar axis set about two degrees low and the second image shows trails with the polar axis set about two and a half degrees high. For the first image the drift is from left to right; since this drift must be clockwise in the northern hemisphere we deduce that the radius of this arc is downwards, indicating an offset of the telescope mount axis below the pole. Similarly, the radius of the arc in the second image must be upwards. But note that something strange has happened - the only adjustment to the mount between these two exposures was in the elevation of the polar axis, so why aren't the trails in the second image roughly horizontal like those in the first?
The answer is that the telescope and image sensor had rotated anti-clockwise slightly between the two exposures whilst attempting to track the stars. Therefore, although the bottom edge of the sensor was aligned as accurately as possible with the horizon for the first exposure, it was at a slight angle for the second exposure. King emphasises that the images should be viewed at the same angle as that for which they were exposed, so if the second image is rotated slightly anti-clockwise to match its orientation during the exposure, the lines would indeed appear to be horizontal.


The next two images are examples of general polar drift: they are for a mount adjusted a small amount west and above the pole (third figure) and a small amount east and above the pole (fourth figure). For a polar offset exactly due west or due east, the trails would be vertical provided that the bottom edge of the image sensor was parallel to the horizon during the exposure.

Some tips for polar adjustment
To avoid misinterpreting the direction of a polar drift trail due to the orientation of the sensor, Attila Mádai has suggested using the standard drift alignment method for the azimuthal adjustment and the polar drift method for the elevation adjustment. This is likely to appeal to those who are already familiar with the standard drift alignment technique. You can find his discussion of the method at his Telescope Drive Master website. Once the azimuth adjustment has been made, a polar field can be used for the elevation adjustment - any remaining drift must be due to elevation error alone so the length of the trail is the only important factor, not its direction.
To make the elevation adjustment, select a star close to the pole and use either a reticle eyepiece or a video camera or webcam for which the image scale is known. Be certain which way the star is expected to move - test this by giving the telescope tube a little nudge in the desired direction; if a polar star is used and the elevation of the mount is being raised, nudge the front of the tube upwards for example. Then adjust the elevation of the mount so that the star moves in the correct direction in the eyepiece or video image by the appropriate amount.
Summary
The two main advantages of the polar drift method are:
- It permits accurate alignment with the refracted pole because trails of stars at or near the pole are used and they are therefore all affected similarly by refraction. There is none of the frustration of the standard method, where a star whose position is affected more and more by refraction is followed until it disappears into the horizon murk, without ever finding an adjustment that reduces the drift to nothing.
- The length and orientation of the drift trail gives information about the size and direction of the polar offset. In principle it is possible to adjust the elevation and azimuth based on just one measurement rather than the measurements in two different directions that the standard drift method requires. However, an iterative technique is likely to be needed in practice.
Those already familiar with the standard drift alignment technique may prefer to use declination drift for a star on the meridian at the celestial equator for the azimuth adjustment and then use the polar drift method to gain a quick and accurate elevation alignment.
Where to align the telescope mount's polar axis?
We have seen how to use the standard declination drift method and King's polar drift method to place the telescope mount axis near to, or at, the refracted pole. But should we adjust this to the true pole instead? What effect does refraction have on the apparent motion of a star as it crosses the sky? Is there an optimum adjustment in elevation to allow for the effects of refraction, and if so, what is it? For the answer to the final piece of our puzzle we need to travel back to Harvard Observatory in the late 1890s for further work by Edward Skinner King.