Declination drift with refraction
In the first part we saw how stellar drift arose through misalignment of the telescope mount's polar axis in the absence of the atmosphere. But we can't ignore it: the rays of light from any star we use for drift alignment are refracted, so the star's position appears to change as a result. Refraction raises the apparent altitude of any star right the way up to the zenith, but the effect becomes increasingly large nearer the horizon. We can see this in the following diagram, which shows the celestial equator at a mid-latitude looking due west in the northern hemisphere, or due east in the southern hemisphere.

The celestial equator is shown by the black line. The blue dots represent a star on the celestial equator at two different times. Refraction raises the star to some new position, shown by the red dots. When the star is lower, it is raised by a greater amount. The increase in apparent altitude also affects the apparent declination, shown by the red arrows. If we look east or west and adjust the elevation of the telescope axis until there is no declination drift in the target star, then the right ascension direction will lie parallel to the dotted red line and the polar axis will point orthogonally to it. In other words, the mount will be aligned such that the polar axis points above the true pole. But where exactly does it point? We will look at that next.
Consequences of refraction for elevation adjustment
We can use the drift alignment spreadsheet to see how refraction affects the apparent position of a star. The following graph shows how the apparent declination increases for a star on the celestial equator (0 degrees declination) as it approaches the western horizon, for different elevations of the mount's polar axis. This is for a latitude of 45 degrees, where the pole has an altitude of 45 degrees. In this example, the star is always at a lower altitude than the pole: at the left-hand end of the curves where the azimuth is 225 degrees, the altitude of the star is 35 degrees; at the right-hand end where the azimuth is 260 degrees, the altitude is only 10 degrees. (By the time the star reaches due west at an azimuth of 270 degrees, it is on the horizon, so when drift-aligning on stars near or below the celestial equator we need to observe them some distance away from due east or west). When we drift align, we aim to reduce the declination drift to zero over as long a period as we can. So we would tend to adjust the mount to an elevation matching the blue curve, i.e. slightly above the refracted pole.

The next graph shows the variation in apparent declination for a star at a declination of 30 degrees, rather than on the celestial equator as in the previous example. In this case, the star is at an altitude of 70 degrees at an azimuth of 225 degrees, 45 degrees at 270 degrees and drops to an altitude of 10 degrees at an azimuth of 300 degrees. So until the star exceeds an azimuth of 270 degrees, it is always at a higher altitude than the pole, contrary to the previous example. Adjusting the elevation of the polar axis to give zero declination drift for as long as possible in this case would require the mount elevation to be slightly below the refracted pole, resulting in the blue curve.
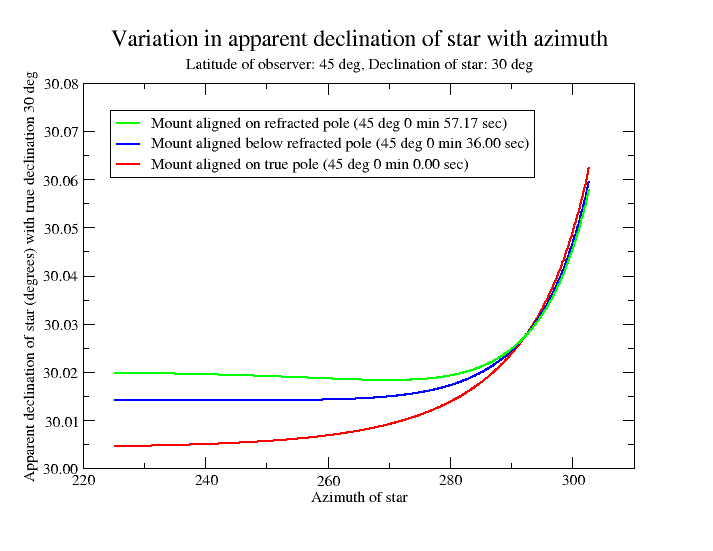
Now look carefully at the green curve in the above graph. Notice how it flattens briefly at an azimuth of about 270 degrees. At that point, the star is at the same altitude as the refracted pole and is affected by the same amount as the refracted pole, giving zero declination drift for a short period. (It's just a coincidence in this example that it happens when the star is due west).
Accuracy of elevation adjustment
The accuracy of the elevation adjustment is hard to quantify because it depends on the altitude of the chosen drift star as seen in the graphs above. In the first case, for a star at elevation 0 degrees and a latitude of 45 degrees, the telescope axis could be adjusted to an altitude of 45d 01m 40.8s, or for a star at an elevation of 30 degrees, the telescope axis might be at 45d 00m 36.0s, a difference of 00d 01m 04.8s. So a typical uncertainty might be +/- 30s, say, but even then, whilst being close to the pole, the telescope axis is pointing nowhere in particular.
Choice of star for elevation adjustment
Ideally, the elevation adjustment should be made using a star at an angle of 90 degrees relative to that used for the azimuth adjustment. This gives the maximum drift rate due to the elevation error and minimises the dependency on any errors in azimuth. In other words, we should try to choose a star at an hour angle of about 6 or 18 hours.
The 6 hour/18 hour great circle cuts the horizon due east and due west and a star at zero degrees declination would be on the horizon at that point. So we often we hear the advice to "pick a star above the east/west horizon at an altitude of 30 degrees". This is good advice because it avoids the worst effects of refraction, but such a star is no longer at 90 degrees to the meridian direction, being closer to the meridian than this ideal location. So any error in the mount's azimuthal alignment will also contribute to the drift and it will be necessary to iterate between the azimuthal and elevation adjustments.
In general, if we adjust the elevation axis to obtain long periods of zero or very small declination drift, the following will be the case:
- The elevation axis points above the refracted pole for a drift star at a lower altitude than the refracted pole.
- The elevation axis points below the refracted pole for a drift star at a higher altitude than the refracted pole.
- The elevation axis points at the refracted pole for a drift star at the same altitude as the refracted pole (but the duration of zero drift may only be fairly short in this case).
- A drift-aligned elevation axis will never lie below the true pole.
As we have seen in the above graphs, the rate of drift does depend on the altitude and azimuth of the chosen star so try to pick a star at a similar altitude and azimuth each time the drift for the elevation adjustment is measured. Otherwise the adjustment to get zero drift will vary each time we do it. This is one of the reasons why the elevation adjustment is often abandoned after a long period of drift alignment with the nagging feeling that something isn't quite right.
Consequences of refraction for azimuth adjustment
Refraction does not have a significant effect on the azimuthal adjustment of the mount's polar axis because we are measuring the star's drift as it crosses the meridian in that case. The star is highest in the sky when it crosses the meridian so is least affected by refraction at that point. In addition, the shift caused by refraction is roughly constant along the star's path for half an hour or so each side of the meridian. For example, a star on the celestial equator at 45 degrees latitude has an altitude of 45 degrees on the meridian. Half an hour earlier or later, the altitude is about 44.5 degrees. Refraction increases the star's apparent altitude by about 0.02 arc seconds more at 44.5 degrees altitude than it does at 45 degrees altitude - a completely negligible effect for the purposes of drift alignment.
Choice of star for azimuth adjustment
We should make the azimuth adjustment using a star at an hour angle of 0 hours, i.e. on the meridian. This maximises the rate of drift for any given error in azimuth and minimises the dependency on any errors in elevation. In other words, even if there is an elevation error, the azimuth will be correct once the rate of drift on the meridian is very close to zero. Because we want to measure the drift rate as the star crosses the meridian, we can start at a location a little bit to the east and follow it until it is the same distance to the west. A star on the celestial equator is a good choice, but we can pick something at a higher declination if we need to avoid obstructions. As we saw on the equations page, the rate of drift (neglecting refraction) is independent of the star's true declination unless the distance from the pole is small enough for the polar misalignment to become significant. Therefore we are not constrained to choose a star on the celestial equator - it has no effect on our ability to measure the drift rate.
Accuracy of azimuth adjustment
It is interesting to consider the accuracy with which we can make the azimuth adjustment. If we use the traditional drift alignment method, we observe a star for a while and note the drift, then tweak the azimuth a bit and observe the drift again, and continue this process until the drift is too small to measure over the length of time that we observe the star. We can use the spreadsheet to see the range of azimuth of the mount's polar axis for which the drift is less than our smallest measurable value. This give us some idea of the likely accuracy of our adjustment. The following table shows the uncertainties for two different minimum drifts at a latitude of 45 degrees, with no elevation error.
| Latitude (degrees) | Smallest measurable drift (arcsec in ten minutes) | Drift rate (arcsec per second) | Uncertainty in azimuth adjustment (dd:mm:ss) |
|---|---|---|---|
| 45 | 5 | 0.008333 | +/- 00:02:42 |
| 45 | 1 | 0.001667 | +/- 00:00:33 |
The table shows us that if we creep up on the correct azimuth by making a series of tiny adjustments then we will stop 2 minutes 42 seconds away from the correct azimuth if the smallest drift we can measure is 5 arc seconds in 10 minutes, or 33 seconds away if we can measure down to 1 arc second in ten minutes. In practice our final adjustment will land us somewhere within the range of uncertainty rather than at one edge. Of course, we can increase the accuracy if we measure the drift over a longer period, giving a smaller drift rate.
These figures also give us an idea of the likely accuracy if we use the spreadsheet to calculate the telescope axis position based on the measured drift. If the uncertainty in our drift measurement is 1 arcsec in ten minutes, then we can't expect to align the axis to better than half an arc minute in azimuth. You can make similar calculations for your own latitude.
Drift align in the east or west?
So far we have assumed that performing the elevation adjustment by drift aligning in the east or west both give equivalent results. In principle they do, but if we are doing traditional drift alignment by tweaking the elevation in response to any drift then there is an important difference. In the east, stars are rising, so the effects of refraction decrease and we should approach an increasingly consistent alignment. In the west, stars are setting and the effects of refraction get worse, so we may never settle on a period of zero drift before a star disappears into the murk. It is better to align to the east if we can.
Polar drift trails - a better method of elevation adjustment
Given the difficulties outlined above, adjusting the elevation of a telescope mount by the standard declination drift method looks like a bit of a mess. There doesn't seem to be an easy way to do it, or to know exactly where we've aligned the elevation axis to when we've done it. But we noted above that alignment using a star at the same altitude as the refracted pole would give an alignment on the refracted pole. So how might we do that? Fortunately the answer was provided by Edward Skinner King in his book "A Manual of Celestial Photography" in 1931, as we shall see next.